Common Core Standards - Ratios and Proportional Relationships

Mathematics - Common Core Standards

Ratios and Proportional Relationships - Grade 6

Understand ratio concepts and use ratio reasoning to solve problems.

CCSS.MATH.CONTENT.6.RP.A.1
Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities. For example, "The ratio of wings to beaks in the bird house at the zoo was 2:1, because for every 2 wings there was 1 beak." "For every vote candidate A received, candidate C received nearly three votes."

Ratio Relationships

Ratio Basics

CCSS.MATH.CONTENT.6.RP.A.2
Understand the concept of a unit rate a/b associated with a ratio a:b with b ≠ 0, and use rate language in the context of a ratio relationship. For example, "This recipe has a ratio of 3 cups of flour to 4 cups of sugar, so there is 3/4 cup of flour for each cup of sugar, so there is 3/4 cup of flour for each cup of sugar." or "We paid $75 for 15 hamburgers, wich is a rate of $5 per hamburger."

Unit Rates with Price Per 1 Item

Unit Rate

Unit Cost

CCSS.MATH.CONTENT.6.RP.A.3
Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.

	Basic Tape Diagrams
	Tape Diagrams
	Ratio Word Problems with Tape Diagrams
	More Word Problems with Tape Diagrams
	Double Number Lines

CCSS.MATH.CONTENT.6.RP.A.3.A
Make tables of equivalent ratios relating quantities with whole-number measurements, find missing values in the tables, and plot the pairs of values on the coordinate plane. Use tables to compare ratios.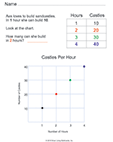

Ratios, Tables and Graphs

CCSS.MATH.CONTENT.6.RP.A.3.B
Solve unit rate problems including those involving unit pricing and constant speed. For example, if it took 7 hours to mow 4 lawns, then at that rate, how many lawns could be mowed in 35 hours? At what rate were lawns being mowed?

Unit Rate / Constant Speed

CCSS.MATH.CONTENT.6.RP.A.3.C
Find a percent of a quantity as a rate per 100 (e.g., 30% of a quantity means 30/100 times the quantity); solve problems involving finding the whole, given a part and the percent.

Tape Diagrams and Percentages

CCSS.MATH.CONTENT.6.RP.A.3.D
Use ratio reasoning to convert measurement units; manipulate and transform units appropriately when multiplying or dividing quantities.

Convert Pints to Cups

The Common Core State Standards are © Copyright 2010. National Governors Association Center for Best Practices and Council of Chief State School Officers. All rights reserved. For more information about the Common Core State Standards, visit their website at http://www.corestandards.org

Click on any of the standards on the left to create custom worksheets or to print premade materials.