 Adaptive Worksheets
Adaptive Worksheets
Helping Every Child to Succeed
toll-free (888) 777-0876
fax (888) 777-0875
Math - Common Core Standards
Fourth Grade
Number and Operations in Base Ten - Fractions
Extend Understanding of Fraction Equivalence and Ordering
4.NF.A.1Explain why a fraction a/b is equivalent to a fraction (n × a)/(n × b) by using visual fraction models, with attention to how the number and size of the parts differ even though the two fractions themselves are the same size. Use this principle to recognize and generate equivalent fractions.
 |
Fractions of 100 and Some Equivalents |
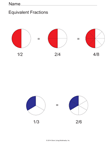 |
Fraction Equivalents |
 |
Fraction Equivalents |
4.NF.A.2
Compare two fractions with different numerators and different denominators, e.g., by creating common denominators or numerators, or by comparing to a benchmark fraction such as 1/2. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.
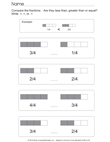 |
Fraction Comparison - Unequal Fractions |
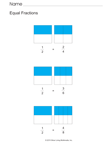 |
Fraction Comparison - Equal Fractions |
 |
Equivalent Fractions |
 |
Compare Fractions |
Build fractions from unit fractions.
4.NF.B.3
Understand a fraction a/b with a > 1 as a sum of fractions 1/b.
Understand a fraction a/b with a > 1 as a sum of fractions 1/b.
4.NF.B.3.A
Understand addition and subtraction of fractions as joining and separating parts referring to the same whole.
Understand addition and subtraction of fractions as joining and separating parts referring to the same whole.
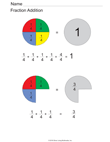 |
Fraction Addition |
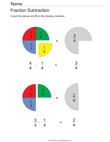 |
Fraction Subtraction |
4.NF.B.3.B
Decompose a fraction into a sum of fractions with the same denominator in more than one way, recording each decomposition by an equation. Justify decompositions, e.g., by using a visual fraction model. Examples: 3/8 = 1/8 + 1/8 + 1/8 ; 3/8 = 1/8 + 2/8 ; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8.
Decompose a fraction into a sum of fractions with the same denominator in more than one way, recording each decomposition by an equation. Justify decompositions, e.g., by using a visual fraction model. Examples: 3/8 = 1/8 + 1/8 + 1/8 ; 3/8 = 1/8 + 2/8 ; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8.
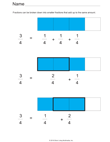 |
Decompose 3/4 into Smaller Fractions |
4.NF.B.3.C
Add and subtract mixed numbers with like denominators, e.g., by replacing each mixed number with an equivalent fraction, and/or by using properties of operations and the relationship between addition and subtraction.
Add and subtract mixed numbers with like denominators, e.g., by replacing each mixed number with an equivalent fraction, and/or by using properties of operations and the relationship between addition and subtraction.
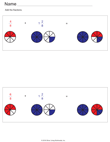 |
Add Mixed Numbers |
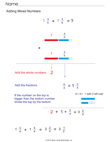 |
Add Mixed Numbers |
 |
Convert a Whole Number to a Mixed Number |
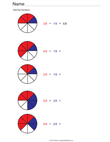 |
Add Fractions with Like Denominators (Prep for Mixed Number Addition) |
4.NF.B.3.D
Solve word problems involving addition and subtraction of fractions referring to the same whole and having like denominators, e.g., by using visual fraction models and equations to represent the problem.
Solve word problems involving addition and subtraction of fractions referring to the same whole and having like denominators, e.g., by using visual fraction models and equations to represent the problem.
 |
Addition of Fractions Word Problems |
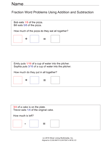 |
Addition and Subtraction Word Problems |
 |
Fraction Word Problems Using Multiplication |
4.NF.B.4
Apply and extend previous understandings of multiplication to multiply a fraction by a whole number.
Apply and extend previous understandings of multiplication to multiply a fraction by a whole number.
4.NF.B.4.A
Understand a fraction a/b as a multiple of 1/b. For example, use a visual fraction model to represent 5/4 as the product 5 × (1/4), recording the conclusion by the equation 5/4 = 5 × (1/4).
Understand a fraction a/b as a multiple of 1/b. For example, use a visual fraction model to represent 5/4 as the product 5 × (1/4), recording the conclusion by the equation 5/4 = 5 × (1/4).
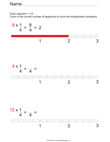 |
Multiply Fractions Using a Visual Model |
4.NF.B.4.B
Understand a multiple of a/b as a multiple of 1/b, and use this understanding to multiply a fraction by a whole number. For example, use a visual fraction model to express 3 × (2/5) as 6 × (1/5), recognizing this product as 6/5. (In general, n × (a/b) = (n × a)/b.)
Understand a multiple of a/b as a multiple of 1/b, and use this understanding to multiply a fraction by a whole number. For example, use a visual fraction model to express 3 × (2/5) as 6 × (1/5), recognizing this product as 6/5. (In general, n × (a/b) = (n × a)/b.)
 |
Multiply Fractions |
4.NF.B.4.C
Solve word problems involving multiplication of a fraction by a whole number, e.g., by using visual fraction models and equations to represent the problem. For example, if each person at a party will eat 3/8 of a pound of roast beef, and there will be 5 people at the party, how many pounds of roast beef will be needed? Between what two whole numbers does your answer lie?
Solve word problems involving multiplication of a fraction by a whole number, e.g., by using visual fraction models and equations to represent the problem. For example, if each person at a party will eat 3/8 of a pound of roast beef, and there will be 5 people at the party, how many pounds of roast beef will be needed? Between what two whole numbers does your answer lie?
 |
Fraction Multiplication Word Problems |
Understand decimal notation for fractions, and compare decimal fractions.
4.NF.C.5
Express a fraction with denominator 10 as an equivalent fraction with denominator 100, and use this technique to add two fractions with respective denominators 10 and 100.For example, express 3/10 as 30/100, and add 3/10 + 4/100 = 34/100.
Express a fraction with denominator 10 as an equivalent fraction with denominator 100, and use this technique to add two fractions with respective denominators 10 and 100.For example, express 3/10 as 30/100, and add 3/10 + 4/100 = 34/100.
 |
Convert Tenths to Hundredths |
4.NF.C.6
Use decimal notation for fractions with denominators 10 or 100. For example, rewrite 0.62 as 62/100; describe a length as 0.62 meters; locate 0.62 on a number line diagram.
Use decimal notation for fractions with denominators 10 or 100. For example, rewrite 0.62 as 62/100; describe a length as 0.62 meters; locate 0.62 on a number line diagram.
 |
Fractions to Decimal Notation - Tenths |
 |
Fractions to Decimal Notation - Hundredths |
4.NF.C.7
Compare two decimals to hundredths by reasoning about their size. Recognize that comparisons are valid only when the two decimals refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual model.
Compare two decimals to hundredths by reasoning about their size. Recognize that comparisons are valid only when the two decimals refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual model.
 |
Compare Decimals on A Numberline |
 |
Arrange Decimals On A Numberline |
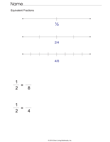 |
Equivalent Fractions On A Numberline |
Click on any of the standards on the left to create custom worksheets or to print premade materials.